트리, Tree with golang

요약

• 루트 노드에서 시작하여 여러 자식 노드가 계층적으로 연결되는 형태의 자료구조이다.

내용

특징

• 계층적 구조를 가지는 비선형 자료구조이다.
• 루트 노드에서 시작하여 여러 자식 노드가 계층적으로 연결되는 형태를 가진다.
• 순환이 없는 연결 구조이다.

핵심 개념

• 루트 노드
  • 트리의 최상위 노드로 부모가 없는 첫 번째 노드이다.
• 자식 노드
  • 특정 노드 아래에 연결된 하위 노드이다.
• 부모 노드
  • 특정 노드를 연결하는 상위 노드이다.
• 잎 노드
  • 자식 노드가 없는 최종 노드로 트리 끝에 위치한 노드이다.
• 형제 노드
  • 동일한 부모 노드를 가진 노드이다.
• 높이
  • 루트에서 잎 노드까지 가장 긴 경로 길이이다.
• 레벨
  • 트리의 계층을 나타내는 깊이로 루트는 0레벨, 그 아래 노드들은 레벨이 1씩 증가한다.

주요 연산

• 삽입
• 삭제
• 검색
• 순회
  • 트리의 모든 노드를 방문하는 연산으로 주소 다음과 같은 방식으로 순회한다.
    • 
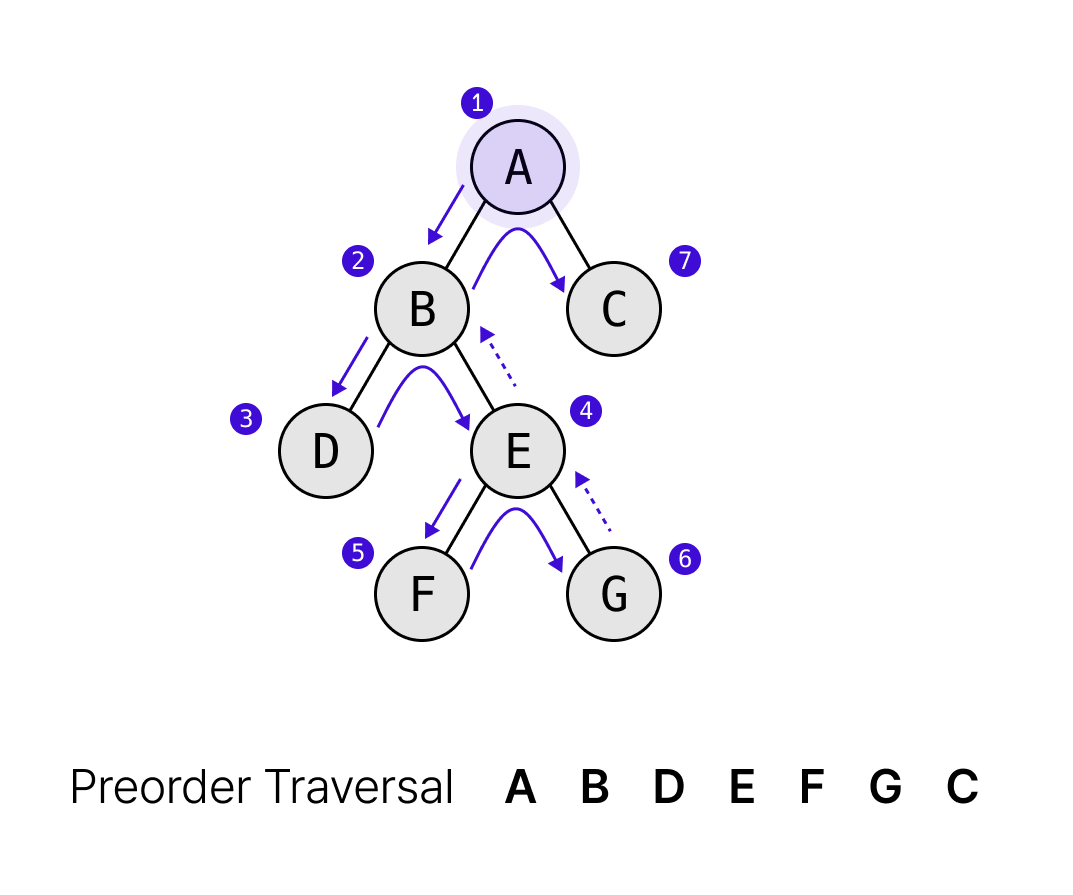
      • 전위 순회: 부모 > 왼쪽 자식 > 오른쪽 자식
    • 
      • 중위 순회: 왼쪽 자식 > 부모 > 오른쪽 자식
    • 
      • 후위 순회: 왼쪽 자식 > 오른쪽 자식> 부모
    • 
      • 레벨 순회: 각 레벨의 노드를 왼쪽에서 오른쪽 순서로 방문

종류

• 이진 트리
  • 각 노드가 최대 두 개의 자식 노드를 가지는 트리이다.
• 이진 탐색 트리
  • 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 큰 값을 가지는 이진트리이다.
• 완전 이진 트리
  • 마지막 레벨을 제외한 모든 레벨이 꽉 차 있고, 마지막 레벨은 왼쪽부터 채워진 이진 트리입니다.
• 균형 이진 트리
  • 모든 잎 노드의 깊이가 비슷하게 유지되는 트리이다.
• N진 트리
  • 각 노드가 최대 N개의 자식을 가질 수 있는 트리이다.

예시

• 프로그램의 추상구문
• 파일시스템

구현체

package main
 
import "fmt"
 
type Node struct {
	value int
	left  *Node
	right *Node
}
 
type BinarySearchTree struct {
	root *Node
}
 
// 새로운 노드 삽입
func (bst *BinarySearchTree) Insert(value int) {
	bst.root = insertNode(bst.root, value)
}
 
func insertNode(node *Node, value int) *Node {
	// 노드가 없다면
	if node == nil {
		return &Node{value: value}
	}
 
	if value < node.value {
		// 노드의 값보다 크면 좌측
		node.left = insertNode(node.left, value)
	} else if value > node.value {
		// 노드의 값보다 작으면 우측
		node.right = insertNode(node.right, value)
	}
	return node
}
 
// 노드 검색
func (bst *BinarySearchTree) Search(value int) bool {
	return searchNode(bst.root, value)
}
 
func searchNode(node *Node, value int) bool {
	if node == nil {
		return false
	}
	if value == node.value {
		return true
	} else if value < node.value {
		// 노드의 값보다 크면 좌측 탐색
		return searchNode(node.left, value)
	} else {
		// 노드의 값보다 작으면 우측 탐색
		return searchNode(node.right, value)
	}
}
 
// 중위 순회, 이진 탐색 트리라서
func (bst *BinarySearchTree) InOrderTraversal() {
	inOrder(bst.root)
	fmt.Println()
}
 
func inOrder(node *Node) {
	if node != nil {
		inOrder(node.left)
		fmt.Print(node.value, " ")
		inOrder(node.right)
	}
}
 
func main() {
	bst := &BinarySearchTree{}
 
	bst.Insert(5)
	bst.Insert(3)
	bst.Insert(7)
	bst.Insert(2)
	bst.Insert(4)
	bst.Insert(6)
	bst.Insert(8)
 
	fmt.Print("inOrder result:")
	bst.InOrderTraversal()
 
	fmt.Println("Does tree has 5?", bst.Search(5))
	fmt.Println("Does tree has 7?", bst.Search(7))
}

참고